In Texas Hold’em poker, a Royal Flush is the best possible hand you can have.
It consists of the Ace, King, Queen, Jack, and Ten of the same suit.
If you’re dealt an Ace and Queen of hearts, you’re two cards away from a Royal Flush.
The remaining cards you need are the King, Jack, and Ten of hearts.
How to Calculate Odds of a Royal Flush with Any 2 Cards Pre-Flop
There are 50 cards left in the deck (since you have 2), and you need 3 specific cards.
The odds of getting each of these cards are as follows:
- The odds of the first card being a King, Jack, or Ten of hearts is 3 out of 50.
- If you get one of these cards, the odds of the next card being one of the remaining two needed cards is 2 out of 49.
- If you get two of these cards, the odds of the final card being the last card you need is 1 out of 48.
To get the total odds, you multiply these together.
However, because the order in which you get these cards doesn’t matter, you also have to consider the different combinations in which you can get these cards.
Combination Formula
The combinatorics formula you’re referring to is known as the “combination” formula, often denoted as “n choose k” or “n C k”. It’s used to calculate the number of ways you can choose k items from a larger set of n items, where the order of selection does not matter.
The formula for combinations is:
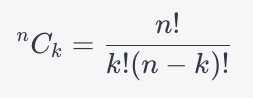
Where n! denotes the factorial of n, which is the product of all positive integers up to n, and k! and (n-k)! are the factorials of k and n-k, respectively.
In your case, you’re looking at “5 choose 3” or 5 C 3. Let’s plug the numbers into the formula:

The factorial of 5, or , is 5*4*3*2*1 = 120. The factorial of 3, or 3!, is 3*2*1 = 6, and the factorial of 2, or 2!, is 2*1 = 2.
So, the calculation becomes:

This means there are 10 different ways to choose 3 items from a set of 5.
So…
Odds of a Royal Flush with Any 2 Cards Pre-Flop = 1/50 * 1/49 * 1/48 * 10 = 0.00085% = 1 in 11,760
Related


